当前位置：首页 > news >正文

做网站原型图/网站推广的软件

news 2025/7/1 0:29:00

做网站原型图,网站推广的软件,阿里云做网站的代码,wordperss网站做负载均衡AVL树简介二叉搜索树在树较为平衡状态下，可以有效的提高数据的插入、删除、查询效率，但是不可避免二叉搜索树随着数据的插入、删除有可能会变为链表结构（利用有序的数据源依次添加），极大的降低效率，所以二…

AVL树简介

二叉搜索树在树较为平衡状态下，可以有效的提高数据的插入、删除、查询效率，但是不可避免二叉搜索树随着数据的插入、删除有可能会变为链表结构（利用有序的数据源依次添加），极大的降低效率，所以二叉搜索树最好时时刻刻都在相对平衡状态，也就是AVL的由来。
AVL树也称为平衡二叉树，AVL树是一种特殊的二叉搜索树，特点是：树种任意节点的左右子树的最大高度差为1。
如果对树与二叉搜索树不熟悉的话，可以查看我的另一篇博客：Java数据结构之二叉树
在这里插入图片描述
上面的两棵树，左边的是AVL树，它的任何节点的两个子树的高度差别都<=1；而右边的不是AVL树，因为5的两颗子树的高度相差为2(以4为根节点的树的高度是3，而以7为根节点的树的高度是1)。

旋转的定义

旋转是以某节点为进行旋转，然后相关节点进行重新关联的操作，旋转分为左旋以及以及右旋:
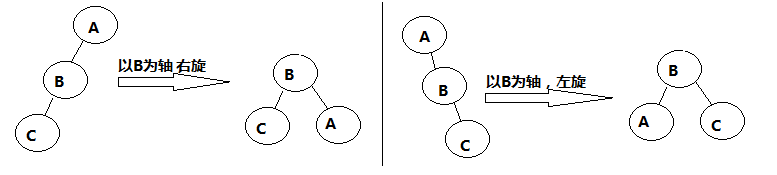
在这里插入图片描述
在AVL树的旋转大致分为4情况：

左左旋转（LL）
左左旋转也称之为LL旋转，其含义是：节点X左子树比右子树的高度大2，且插入的节点位于节点（X）的左子节点（XL）的左子树（T1）上。
右右旋转（RR）
右右旋转也称之为RR旋转，其含义是：节点X右子树比左子树的高度大2，且插入的节点位于节点（X）的右子节点（XL）的右子树（T3）上。
左右旋转（LR）
左右旋转也称之为LR旋转，其含义是：节点X左子树比右子树的高度大2，且插入的节点位于节点（X）的左子节点（XL）的右子树上。
右左旋转（RL）
右左旋转也称之为RL旋转，其含义是：节点X右子树比左子树的高度大2，且插入的节点位于节点（X）的右子节点（XL）的左子树上。

AVL树实现

节点类定义

	 package com.lxx.tree;/*** AVL树节点类定义*@author lxx*/public class AVLTreeNode {//数据public int data;//高度，单个node的高度为1，空树高度为-1public int height;//左子节点public AVLTreeNode left;//右子节点public AVLTreeNode right;//构造方法public AVLTreeNode(int data) {this.data = data;this.height= 0;//添加后会自增高度,初始化为0}}

AVL类定义

	package com.lxx.tree;/*** AVL树的实现类* @author lxx*/public class AVLTree {// 记录根节点public AVLTreeNode root;// 结点个数public int size;// 构造方法public AVLTree() {root = null;size = 0;}// 返回树中的节点数量public int size() {return size;}// 判断是否为空public boolean isEmpty() {return root == null;}// 返回节点的高度public int height(AVLTreeNode node) {return node == null ? -1 : node.height;}// 返回根节点public AVLTreeNode getRoot() {return root;}}

4种旋转情况

	/*** 四种旋转方式中的LL旋转, 当是节点左子树的左子树节添加节点造成的不平衡,采用LL情况,节点整体右旋*/public AVLTreeNode llRotate(AVLTreeNode node) {AVLTreeNode nodeLeft = node.left;node.left = nodeLeft.right;nodeLeft.right = node;node.height = Math.max(height(node.right), height(node.left)) + 1;nodeLeft.height = Math.max(height(nodeLeft.left), node.height) + 1;return nodeLeft;}/*** 四种旋转方式中的RR旋转, 当是节点右子树的右子树节添加节点造成的不平衡,采用RR情况,节点整体左旋*/public AVLTreeNode rrRotate(AVLTreeNode node) {AVLTreeNode nodeRight = node.right;node.right = nodeRight.left;nodeRight.left = node;node.height = Math.max(height(node.right), height(node.left)) + 1;nodeRight.height = Math.max(height(nodeRight.right), node.height) + 1;return nodeRight;}/*** 四种旋转方式中的LR旋转, 当是节点左子树的右子树节添加节点造成的不平衡,采用LR情况,显示左子树左旋没然后节点整体右旋*/public AVLTreeNode lrRotate(AVLTreeNode node) {node.left = rrRotate(node.left);// 左子树先左旋return llRotate(node);// 整体右旋}/*** 四种旋转方式中的RL旋转, 当是节点右子树的左子树节添加节点造成的不平衡,采用RL情况,显示左子树右旋旋没然后节点整体左旋*/public AVLTreeNode rlRotate(AVLTreeNode node) {node.right = llRotate(node.right);// 右子树先右旋return rrRotate(node);// 整体左旋}

新增节点

    /*** 插入数据*/public void insert(int data) {root = insert(root, data);size++;}/*** 插入数据,私有递归*/private AVLTreeNode insert(AVLTreeNode node, int data) {if (node == null) {return new AVLTreeNode(data);}if (data > node.data) {// 插入数据位置在当前节点右子树node.right = insert(node.right, data);if (height(node.right) - height(node.left) == 2) {// node右子树高度比node左子树高度大2,发生不平衡if (node.right.data > data) {// 在右子树的左子树上,rl旋转node = rlRotate(node);} else {// 在右子树的左子树上,rr旋转node = rrRotate(node);}}} else if (data < node.data) {// 插入数据位置在当前节点左子树,继续向当前节点的左子节点添加node.left = insert(node.left, data);if (height(node.left) - height(node.right) == 2) {// node左子树高度比node右子树高度大2,发生不平衡if (node.left.data > data) {// 还是在左子树的左子树上,ll旋转node = llRotate(node);} else {// 在左子树的右子树上,lr旋转node = lrRotate(node);}}} else {// 相等,无需再次添加return null;}// 树高度加1node.height = Math.max(height(node.right), height(node.left)) + 1;return node;}

删除节点

    /*** 删除元素*/public void remove(int data) {root = remove(root, data);size--;}/*** 删除节点,私有递归*/private AVLTreeNode remove(AVLTreeNode node, int data) {if (node == null) {return null;}if (data > node.data) {// 删除节点在当前节点的右子树上node.right = remove(node.right, data);if (height(node.left) - height(node.right) == 2) {// 从右侧删除,那么左子数高度比右子树高度大2,不平衡,调整(旋转)节点左子树AVLTreeNode tempNode = node.left;if (height(tempNode.left) > height(tempNode.right)) {// 删除后node的左子树不平衡,并且node左子树的左子树高度比右子树大,LL旋转node = llRotate(node);} else {// 删除后node的左子树不平衡,并且node左子树的右子树高度比左子树大,LR旋转node = lrRotate(node);}}} else if (data < node.data) {// 删除节点在当前节点的左子树上node.left = remove(node.left, data);if (height(node.right) - height(node.left) == 2) {// 从左侧删除,那么右子树高度比左子树高度大2,不平衡,调整(旋转)节点右子树AVLTreeNode tempNode = node.right;if (height(tempNode.left) > height(tempNode.right)) {// 删除后node的右子树不平衡,并且node右子树的左子树高度比右子树大,RL旋转node = rlRotate(node);} else {// 删除后node的右子树不平衡,并且node右子树的右子树高度比左子树大,RR旋转node = rrRotate(node);}}} else {// 相等,找到要删除的元素if (node.left == null && node.right == null) {// 删除的节点为叶子节点node = null;} else if (node.left != null && node.right == null) {// 删除节点有且只有左子节点,左子节点直接上移成为新的node节点node = node.left;node.height = Math.max(height(node.left), height(node.left)) + 1;} else if (node.left == null && node.right != null) {// 删除节点有且只有右子节点,右子节点直接上移成为新的node节点node = node.right;node.height = Math.max(height(node.left), height(node.left)) + 1;} else {// 删除节点有左子节点,还有右子节点,这里找出删除左子树最大节点替换,或者右子树最小节点替换,这里选用左子树最大节点AVLTreeNode temp = node.left;while (temp.right != null) {temp = temp.right;}// 将最大值赋给node节点node.data = temp.data;// 删除最大值节点node.left = remove(node.left, temp.data);// 调整删除后的高度node.height = Math.max(height(node.left), height(node.left)) + 1;}}size--;return node;}

AVL树的遍历

    // 前序遍历public void preOrder(AVLTreeNode node) {if (node != null) {// 根节点System.out.print(node.data + " ");// 左子树遍历preOrder(node.left);// 右子树遍历preOrder(node.right);}}// 中序遍历public void infixOrder(AVLTreeNode node) {if (node != null) {// 左子树遍历infixOrder(node.left);// 根节点System.out.print(node.data + " ");// 右子树遍历infixOrder(node.right);}}// 后序遍历public void postOrder(AVLTreeNode node) {if (node != null) {// 左子树遍历postOrder(node.left);// 右子树遍历postOrder(node.right);// 根节点System.out.print(node.data + " ");}}

测试

	package com.lxx.tree;/*** AVL树测试类* @author lxx*/public class AVLTreeTest {public static void main(String[] args) {//创建树AVLTree avlTree = new AVLTree();//数据源,无序的1~10int[] array = {4,6,1,3,2,7,8,9,5,10};//添加数据for (int i = 0; i < array.length; i++) {avlTree.insert(array[i]);}//前序遍历System.out.print("前序遍历");avlTree.preOrder(avlTree.getRoot());System.out.println();//中序遍历System.out.print("中序遍历");avlTree.infixOrder(avlTree.getRoot());System.out.println();//后序遍历System.out.print("后序遍历");avlTree.postOrder(avlTree.getRoot());System.out.println();//删除5System.out.println("删除5");avlTree.remove(5);//前序遍历System.out.print("前序遍历");avlTree.preOrder(avlTree.getRoot());System.out.println();//中序遍历System.out.print("中序遍历");avlTree.infixOrder(avlTree.getRoot());System.out.println();//后序遍历System.out.print("后序遍历");avlTree.postOrder(avlTree.getRoot());System.out.println();}}

控制台输出在这里插入图片描述

AVL树Java实现完整代码

节点类:

	 package com.lxx.tree;/*** AVL树节点类定义*@author lxx*/public class AVLTreeNode {//数据public int data;//高度，单个node的高度为1，空树高度为-1public int height;//左子节点public AVLTreeNode left;//右子节点public AVLTreeNode right;//构造方法public AVLTreeNode(int data) {this.data = data;this.height= 0;//添加后会自增高度,初始化为0}}

AVL树实现类:

	package com.lxx.tree;/*** AVL树的实现类* @author lxx*/public class AVLTree {// 记录根节点public AVLTreeNode root;// 结点个数public int size;// 构造方法public AVLTree() {root = null;size = 0;}// 返回树中的节点数量public int size() {return size;}// 判断是否为空public boolean isEmpty() {return root == null;}// 返回节点的高度public int height(AVLTreeNode node) {return node == null ? -1 : node.height;}// 返回根节点public AVLTreeNode getRoot() {return root;}/*** 四种旋转方式中的LL旋转, 当是节点左子树的左子树节添加节点造成的不平衡,采用LL情况,节点整体右旋*/public AVLTreeNode llRotate(AVLTreeNode node) {AVLTreeNode nodeLeft = node.left;node.left = nodeLeft.right;nodeLeft.right = node;node.height = Math.max(height(node.right), height(node.left)) + 1;nodeLeft.height = Math.max(height(nodeLeft.left), node.height) + 1;return nodeLeft;}/*** 四种旋转方式中的RR旋转, 当是节点右子树的右子树节添加节点造成的不平衡,采用RR情况,节点整体左旋*/public AVLTreeNode rrRotate(AVLTreeNode node) {AVLTreeNode nodeRight = node.right;node.right = nodeRight.left;nodeRight.left = node;node.height = Math.max(height(node.right), height(node.left)) + 1;nodeRight.height = Math.max(height(nodeRight.right), node.height) + 1;return nodeRight;}/*** 四种旋转方式中的LR旋转, 当是节点左子树的右子树节添加节点造成的不平衡,采用LR情况,显示左子树左旋没然后节点整体右旋*/public AVLTreeNode lrRotate(AVLTreeNode node) {node.left = rrRotate(node.left);// 左子树先左旋return llRotate(node);// 整体右旋}/*** 四种旋转方式中的RL旋转, 当是节点右子树的左子树节添加节点造成的不平衡,采用RL情况,显示左子树右旋旋没然后节点整体左旋*/public AVLTreeNode rlRotate(AVLTreeNode node) {node.right = llRotate(node.right);// 右子树先右旋return rrRotate(node);// 整体左旋}/*** 插入数据*/public void insert(int data) {root = insert(root, data);size++;}/*** 插入数据,私有递归*/private AVLTreeNode insert(AVLTreeNode node, int data) {if (node == null) {return new AVLTreeNode(data);}if (data > node.data) {// 插入数据位置在当前节点右子树node.right = insert(node.right, data);if (height(node.right) - height(node.left) == 2) {// node右子树高度比node左子树高度大2,发生不平衡if (node.right.data > data) {// 在右子树的左子树上,rl旋转node = rlRotate(node);} else {// 在右子树的左子树上,rr旋转node = rrRotate(node);}}} else if (data < node.data) {// 插入数据位置在当前节点左子树,继续向当前节点的左子节点添加node.left = insert(node.left, data);if (height(node.left) - height(node.right) == 2) {// node左子树高度比node右子树高度大2,发生不平衡if (node.left.data > data) {// 还是在左子树的左子树上,ll旋转node = llRotate(node);} else {// 在左子树的右子树上,lr旋转node = lrRotate(node);}}} else {// 相等,无需再次添加return null;}// 树高度加1node.height = Math.max(height(node.right), height(node.left)) + 1;return node;}/*** 删除元素*/public void remove(int data) {root = remove(root, data);size--;}/*** 删除节点,私有递归*/private AVLTreeNode remove(AVLTreeNode node, int data) {if (node == null) {return null;}if (data > node.data) {// 删除节点在当前节点的右子树上node.right = remove(node.right, data);if (height(node.left) - height(node.right) == 2) {// 从右侧删除,那么左子数高度比右子树高度大2,不平衡,调整(旋转)节点左子树AVLTreeNode tempNode = node.left;if (height(tempNode.left) > height(tempNode.right)) {// 删除后node的左子树不平衡,并且node左子树的左子树高度比右子树大,LL旋转node = llRotate(node);} else {// 删除后node的左子树不平衡,并且node左子树的右子树高度比左子树大,LR旋转node = lrRotate(node);}}} else if (data < node.data) {// 删除节点在当前节点的左子树上node.left = remove(node.left, data);if (height(node.right) - height(node.left) == 2) {// 从左侧删除,那么右子树高度比左子树高度大2,不平衡,调整(旋转)节点右子树AVLTreeNode tempNode = node.right;if (height(tempNode.left) > height(tempNode.right)) {// 删除后node的右子树不平衡,并且node右子树的左子树高度比右子树大,RL旋转node = rlRotate(node);} else {// 删除后node的右子树不平衡,并且node右子树的右子树高度比左子树大,RR旋转node = rrRotate(node);}}} else {// 相等,找到要删除的元素if (node.left == null && node.right == null) {// 删除的节点为叶子节点node = null;} else if (node.left != null && node.right == null) {// 删除节点有且只有左子节点,左子节点直接上移成为新的node节点node = node.left;node.height = Math.max(height(node.left), height(node.left)) + 1;} else if (node.left == null && node.right != null) {// 删除节点有且只有右子节点,右子节点直接上移成为新的node节点node = node.right;node.height = Math.max(height(node.left), height(node.left)) + 1;} else {// 删除节点有左子节点,还有右子节点,这里找出删除左子树最大节点替换,或者右子树最小节点替换,这里选用左子树最大节点AVLTreeNode temp = node.left;while (temp.right != null) {temp = temp.right;}// 将最大值赋给node节点node.data = temp.data;// 删除最大值节点node.left = remove(node.left, temp.data);// 调整删除后的高度node.height = Math.max(height(node.left), height(node.left)) + 1;}}size--;return node;}// 前序遍历public void preOrder(AVLTreeNode node) {if (node != null) {// 根节点System.out.print(node.data + " ");// 左子树遍历preOrder(node.left);// 右子树遍历preOrder(node.right);}}// 中序遍历public void infixOrder(AVLTreeNode node) {if (node != null) {// 左子树遍历infixOrder(node.left);// 根节点System.out.print(node.data + " ");// 右子树遍历infixOrder(node.right);}}// 后序遍历public void postOrder(AVLTreeNode node) {if (node != null) {// 左子树遍历postOrder(node.left);// 右子树遍历postOrder(node.right);// 根节点System.out.print(node.data + " ");}}}

测试类:

	package com.lxx.tree;/*** AVL树测试类* @author lxx*/public class AVLTreeTest {public static void main(String[] args) {//创建树AVLTree avlTree = new AVLTree();//数据源,无序的1~10int[] array = {4,6,1,3,2,7,8,9,5,10};//添加数据for (int i = 0; i < array.length; i++) {avlTree.insert(array[i]);}//前序遍历System.out.print("前序遍历");avlTree.preOrder(avlTree.getRoot());System.out.println();//中序遍历System.out.print("中序遍历");avlTree.infixOrder(avlTree.getRoot());System.out.println();//后序遍历System.out.print("后序遍历");avlTree.postOrder(avlTree.getRoot());System.out.println();//删除5System.out.println("删除5");avlTree.remove(5);//前序遍历System.out.print("前序遍历");avlTree.preOrder(avlTree.getRoot());System.out.println();//中序遍历System.out.print("中序遍历");avlTree.infixOrder(avlTree.getRoot());System.out.println();//后序遍历System.out.print("后序遍历");avlTree.postOrder(avlTree.getRoot());System.out.println();}}

查看全文

http://www.jmfq.cn/news/4995001.html