一站式网站建设服务/宁波seo网络推广公司排名
写一篇关于Cholesky分解的文章,作为学习笔记,尽量一文看懂矩阵Cholesky分解,以及用Cholesky分解来求解对称正定线性方程组,以及求对称正定矩阵的逆的应用。
文章目录
- 直接Cholesky分解
- 分块Cholesky分解
- Cholesky分解应用于求解线性方程组,以及矩阵求逆
- 参考资料
先简单理解下正定矩阵和半正定矩阵的定义[1][2][3]:
- 给定一个 n×nn\times nn×n 的实对称矩阵 AAA ,若对于任意长度为 n 的非零向量 X,有 XTAX>0X^TAX \gt 0XTAX>0 恒成立,则矩阵 AAA 是一个正定矩阵。
- 给定一个 n×nn\times nn×n 的实对称矩阵 AAA ,若对于任意长度为 n 的非零向量 X,有 XTAX≥0X^TAX \geq 0XTAX≥0 恒成立,则矩阵 AAA 是一个半正定矩阵。
直接Cholesky分解
定理——若A∈Rn×nA \in R^{n\times n}A∈Rn×n是对称正定矩阵,则存在一个对角元全为正数的下三角矩阵L∈Rn×nL \in R^{n\times n}L∈Rn×n,使得A=LLTA=LL^TA=LLT成立。
LLL是一个下三角形,形式是这样的:
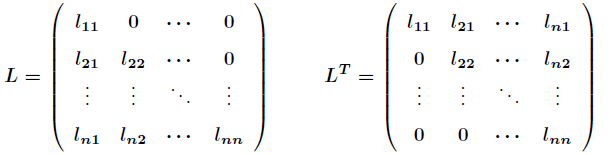
推导A=LLTA=LL^TA=LLT:我们先令
A=[a11A21TA21A22],L=[l110L21L22],LT=[l11L21T0L22T]A = \left[ \begin{matrix} a_{11}&A_{21}^{T}\\ A_{21}&A_{22}\\ \end{matrix} \right], \quad L = \left[ \begin{matrix} l_{11}&0\\ L_{21}&L_{22}\\ \end{matrix} \right], \quad L^{T} = \left[ \begin{matrix} l_{11}&L_{21}^{T}\\ 0&L_{22}^{T}\\ \end{matrix} \right]A=[a11A21A21TA22],L=[l11L210L22],LT=[l110L21TL22T]
其中a11a_{11}a11和l11l_{11}l11是一个标量,A21A_{21}A21和L21L_{21}L21是一个列向量,A22A_{22}A22是一个n-1阶的方阵,而L22L_{22}L22是一个n-1阶的下三角形。那么:
[a11A21TA21A22]=[l110L21L22][l11L21T0L22T]=[l112l11L21Tl11L21L21L21T+L22L22T]\left[ \begin{matrix} a_{11}&A_{21}^{T}\\ A_{21}&A_{22}\\ \end{matrix} \right] = \left[ \begin{matrix} l_{11}&0\\ L_{21}&L_{22}\\ \end{matrix} \right] \left[ \begin{matrix} l_{11}&L_{21}^{T}\\ 0&L_{22}^{T}\\ \end{matrix} \right]= \left[ \begin{matrix} l_{11}^{2}&l_{11}L_{21}^{T}\\ l_{11}L_{21}&L_{21}L_{21}^{T}+L_{22}L_{22}^{T}\\ \end{matrix} \right][a11A21A21TA22]=[l11L210L22][l110L21TL22T]=[l112l11L21l11L21TL21L21T+L22L22T]
未知量只有标量l11l_{11}l11,列向量L21L_{21}L21,和下三角形L22L_{22}L22,也是我们要求的。很容易得到:
l11=a11l_{11} = \sqrt {a_{11}}l11=a11
L21=1l11A21L_{21} = \frac {1}{l_{11}}A_{21}L21=l111A21
L22L22T=A22−L21L21TL_{22}L_{22}^{T} = A_{22} - L_{21}L_{21}^{T} L22L22T=A22−L21L21T
其中l11l_{11}l11,L21L_{21}L21我们直接可以求出来了,并且可以求出A22′=A22−L21L21TA_{22}' = A_{22} - L_{21}L_{21}^{T}A22′=A22−L21L21T。
而A22′=L22L22TA_{22}' = L_{22}L_{22}^{T}A22′=L22L22T又是一个Cholesky分解!被分解的矩阵是一个n-1阶方阵A22′A_{22}'A22′。因此,Cholesky分解算法具有递归性质,每一轮可以求出LLL的一列,依次往下求,就可以把整个L求出来。
一个例子[4]:
另外,上述的方法需要进行开方,这有可能损失精度和增加运算量,为了避免开方,Cholesky分解有个改进的版本。将对称正定矩阵通过分解成A=LDLTA=LDL^TA=LDLT,其中L是单位下三角矩阵(单位下三角矩阵的对角线右上方的系数全部为零,左下方的系数全为一),D是对角均为正数的对角矩阵。把这一分解叫做LDL分解,是Cholesky分解的变形。具体先不展开了,可以参考[5],以及其中的参考代码。
分块Cholesky分解
这一部分其实原理和上面是一样的,只是l11l_{11}l11也是一个矩阵块来做,这样算法就是在一个矩阵块粒度递归往下做,效率上快很多,可以比较容易利用到GPU计算加速。我主要参考了文献[6]的内容,只做一个笔记用。
首先,把AAA矩阵分块,其中A11A_{11}A11是一个r×rr\times rr×r方阵,rrr是我们设定的可以采用直接cholesky分解算法求解的块大小。
类似的,位面可以得到:
其中公式(8)其实我们一般计算的是线性方程组:
S⋅L11T=BS\cdot L_{11}^T = BS⋅L11T=B
其中L11TL_{11}^TL11T是一个上三角形,因此,我们可以比较容易求出S(先直接可以求出S的第一列,然后是第二列,以此类推)。可以直接调用各种BLAS库的trsm函数求解[7]。
公式(9)又是一个Cholesky分解,一直递归下去采用分块Cholesky分解,直到A^−S⋅ST\hat{A}-S\cdot S^TA^−S⋅ST的size小于等于r×rr\times rr×r就不在分解了,最后采用一次直接Cholesky分解。
示意图以及流程总结如下:
到这里就把Cholesky分解的计算方法讲清楚了。
Cholesky分解应用于求解线性方程组,以及矩阵求逆
如果AAA为对称正定矩阵,现在要求解线性方程组AX=BAX=BAX=B:
步骤:
- 求AAA的Cholesky分解,得到A=LLTA=LL^TA=LLT
- 把AXAXAX看成L(LTX)=LYL(L^T X)=LYL(LTX)=LY,求LY=BLY = BLY=B,得到YYY
- 求LTX=YL^T X = YLTX=Y,得到XXX
这样就求出了线性方程组AX=BAX=BAX=B的解XXX。
类似的,如果AAA为对称正定矩阵,我们要求A−1A^{-1}A−1,我们实际上只要求解线性方程组AX=IAX=IAX=I:
步骤:
- 求AAA的Cholesky分解,得到A=LLTA=LL^TA=LLT
- 把AXAXAX看成L(LTX)=LYL(L^T X)=LYL(LTX)=LY,求LY=ILY = ILY=I,得到YYY
- 求LTX=YL^T X = YLTX=Y,得到XXX
这样就求出了逆矩阵X=A−1X= A^{-1}X=A−1。
参考资料
[1] https://www.jiqizhixin.com/articles/2019-03-05-8
[2] https://www.cnblogs.com/marsggbo/p/11461155.html
[3] https://baike.baidu.com/item/%E6%AD%A3%E5%AE%9A%E7%9F%A9%E9%98%B5/11030459?fr=aladdin
[4] https://www.qiujiawei.com/linear-algebra-11/
[5] https://blog.csdn.net/ACdreamers/article/details/44656847
[6] 使用GPU加速计算矩阵的Cholesky分解,沈 聪,高火涛
[7] https://blog.csdn.net/zb1165048017/article/details/70207812






