前言

单应矩阵(Homography)H 它描述了两个平面之间的映射关系。具体的讲，就是处于共同平面上的一些点，在两张图像之间的变换关系。举个例子：空间中有一个长方形盒子，长方形盒子正面中心点为O，用相机在不同的角度拍了两张图片，得到picture1和picture2，且两张图片中都有O点，O点在两张图片中的像素坐标分别为X1(u1,v1)，X2(u2,v2)，你可以简单的认为，这两个坐标之间的关系就是单应性变换，即：X1=HX2(或X2=HX1)
换成齐次坐标，就是：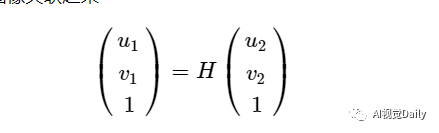
推广到更多点：空间中任意一点，只要都体现在这两张图片上，都满足上面的关系。这里你应该能大致明白单应性矩阵H了。下面我将进行单应矩阵的详细推导

一、VSLAM中单应矩阵的推导

上一篇我们知道了相机模型，我们知道

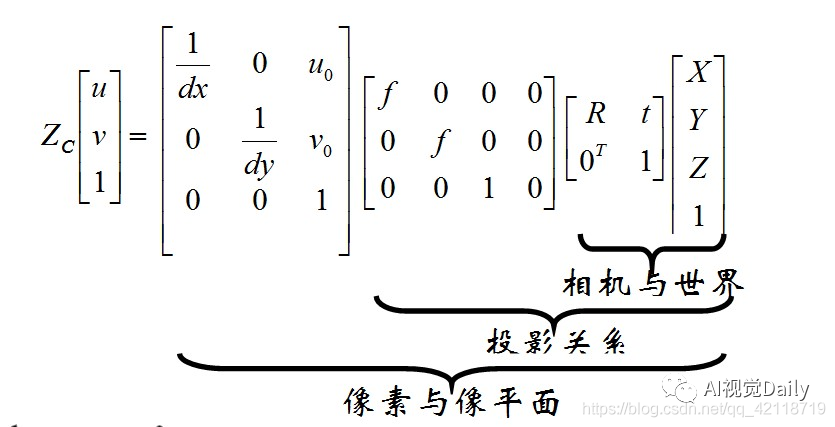
我们知道上面等式右边前两项为相机内参矩阵，我们设为K，则

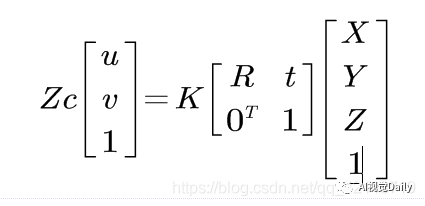
因为旋转矩阵R是3X3，平移矩阵t为3X1，(为了推导方便)把变换矩阵拆成旋转矩阵和平移矩阵：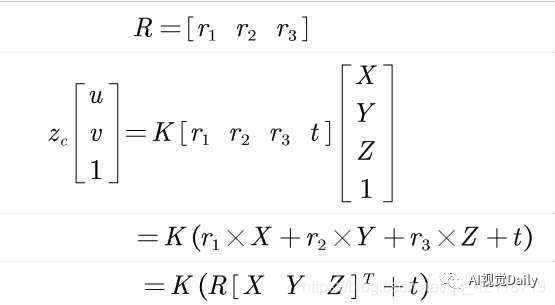

设三维空间中的一点P，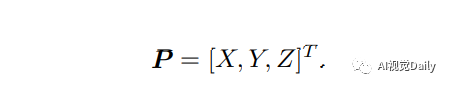
相机最初静止阶段拍了一张图片picture1，这个时候相机的运动无旋转，无平移，R为单位矩阵，t为0，图片中包含P点，则P点在picture1中的像素坐标p1(u1，v1，1)满足：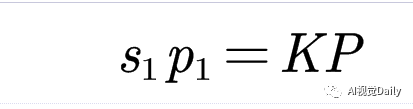
则：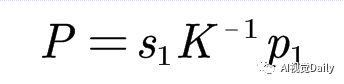
上面这个公式后面会用到

然后相机进行了运动，用旋转矩阵R和平移矩阵描述运动，相机运动后拍了一张图片为picture2，图片包含空间点P，则P点在picture中的像素坐标p2(u2，v2，1)满足：

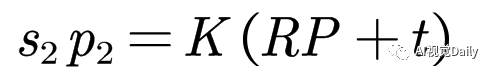
已知p1和p2都来自P，空间P点一定在空间中的一个平面上，空间平面的定义是：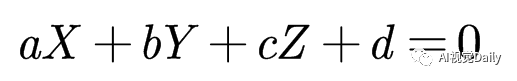
化为矩阵相乘的形式：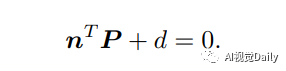
其中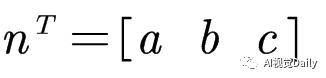
整理可得：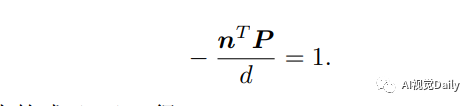
看一下前面p1和p2计算公式，进行下面推导: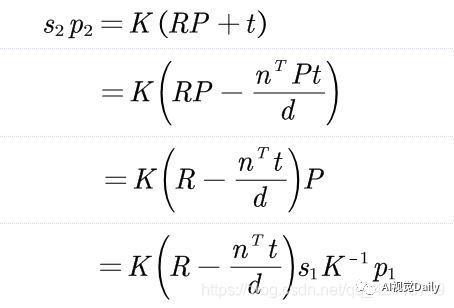
则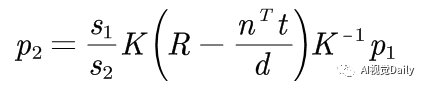
因此可以得到：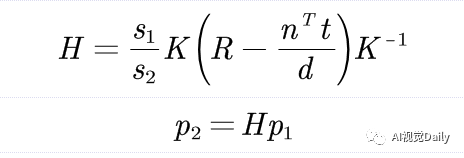

由于齐次坐标p1，p2的尺度不变性，则s1，s2为尺度因子，单应矩阵H为: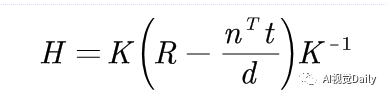

二、单应矩阵的求解

从上面可以看出来单应矩阵与旋转、平移以及平面的参数有关。在齐次坐标下，单应矩阵 H 也是一个 3 × 3 的矩阵，求解时的思路根据匹配点计算 H，然后将它分解可以计算出相机外参旋转矩阵R和平移矩阵t；
把H展开可得：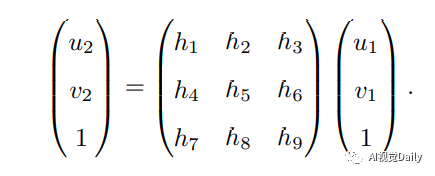
那么在齐次坐标下，H的自由度是多少，H是3x3的，有9个参数，自由度就是9吗？不是9，答案是8,原因如下：
在齐次坐标系的尺度不变性下：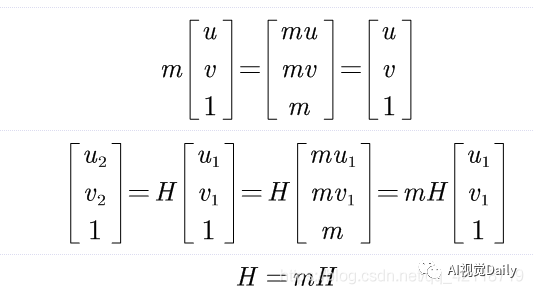
这里m为非零因子，因此可以得到H可以进行任意的缩放而值保持不变，因此H的自由度为8。在求解过程中，通常乘以一个非零因子使得 h9 = 1(在它取非零值时)。然后根据第三行，去掉这个非零因子，这样在矩阵相乘时有：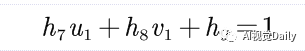
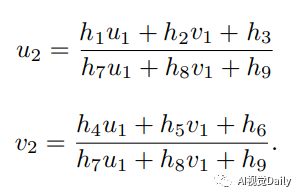
整理得：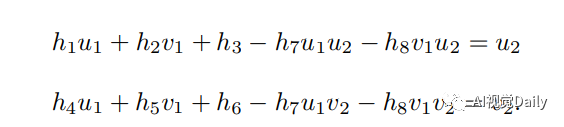
这样一组匹配点对p1和p2就可以构造出两项约束，于是自由度为 8 的单应矩阵可以通过 4 对匹配点算出，即求解以下的线性方程组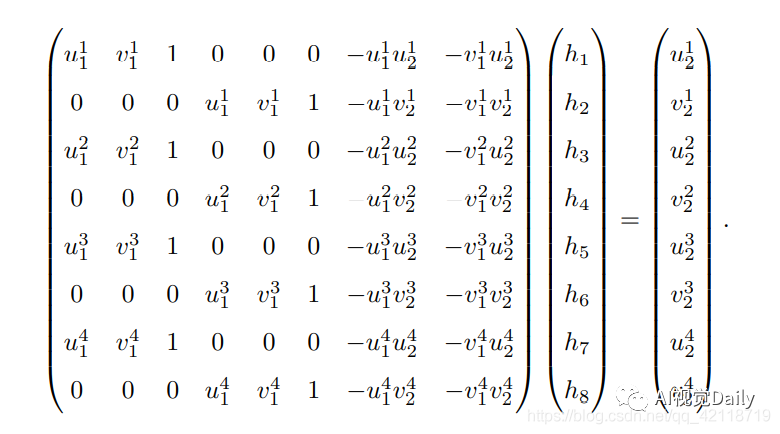
上述方程组采用直接线性解法通常很难得到最优解，所以实际使用中一般会用其他优化方法，如奇异值分解、Levenberg-Marquarat(LM)算法等进行求解。

三、张正友标定中的单应性矩阵

上面我们推导的单应性矩阵是在相机运动的情况下进行的，但是相机标定的过程中相机是静止的，而运动的棋盘格标定板。在张正友标定中，用于标定的棋盘格是三维场景中的一个平面P，其在成像平面的像是另一个平面p，单应性矩阵就是指两个平面之间的映射关系，准确的来说是世界坐标系和像素坐标系之间的映射关系。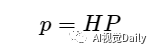

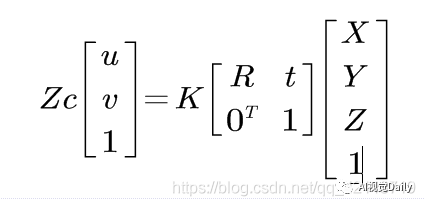
由于齐次坐标的尺度不变性，Zc就变成了尺度因子，则单应性矩阵H为：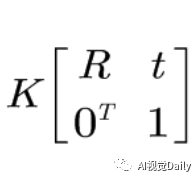

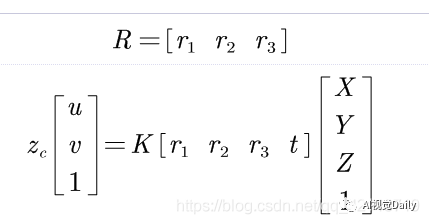
设棋盘格所在的平面为世界坐标系中Z=0的平面，这样棋盘格的任一角点P的世界坐标为(X,Y,0)，根据小孔相机模型：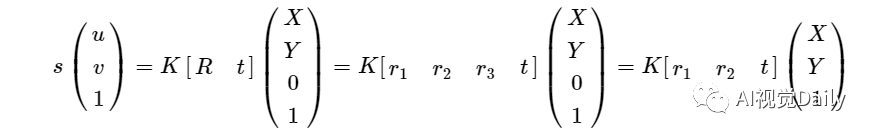
这里的s也是尺度因子，根据平面间的单应性，有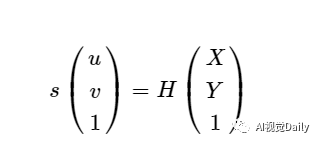
将上面两个等式进行整合，则可以得到单应矩阵H和相机矩阵(包含内参和外参)的相等，如下：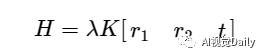
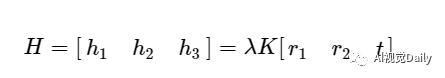
将旋转矩阵R的各个列向量和平移向量t使用H的列向量表示，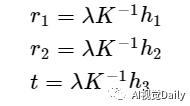
又由于，R是旋转矩阵，则其是正交矩阵，也就是其任意两个列向量的内积为0，列向量的模为1。故有：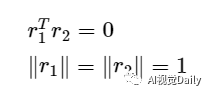
则对于一幅棋盘标定版的图像(一个单应矩阵)可以获得两个对内参数的约束等式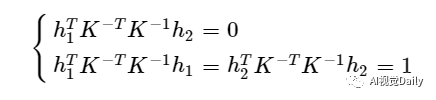

四、根据单应矩阵求解相机内参

根据上面的等式：我们设：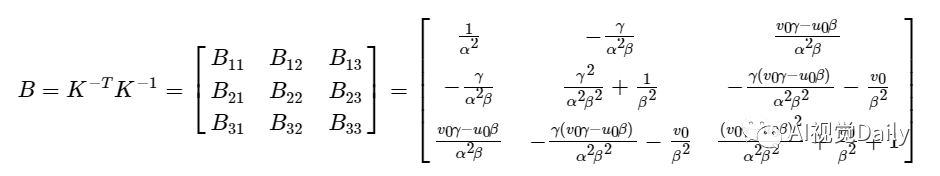

因为方阵乘以方阵的转置得到的是一个对称矩阵，所以矩阵B是一个对称矩阵，其未知量只有6个，将6个未知量写为向量的形式：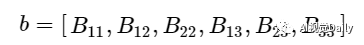
另外我们做如下变化：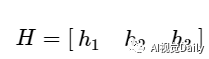
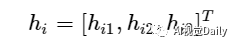
其中i=1，2，3；我们设：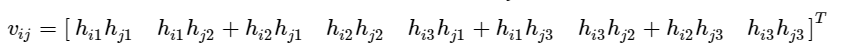
为什么怎么设？我们把下面展开，你会发现Vij包含里面所有的未知量，之所以设成6项，是为了后面与向量b做乘法做铺垫，这里i=1，2，3；j=1，2，3；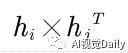
那么约束等式：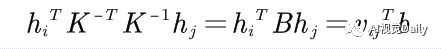
这里你如果不懂：你把下面按照矩阵乘法一项一项的展开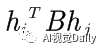
然后你就明白下面等式：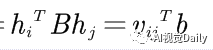
有了上边的等式，再来看从一幅标定板图像得到的等式：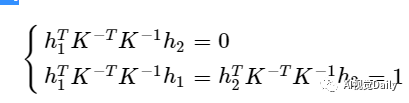
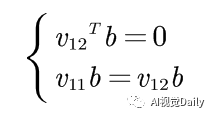
写成矩阵的形式有：

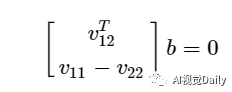
上面的一幅标定板图像取得的约束等式，假如有n幅图像，则

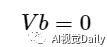
其中，V是一个2n×6的矩阵，b是一个6维向量，所以
当n≥3，可以得到b的唯一解;
当n=2，则可以假设扭曲参数γ=0作为额外的约束条件
当n=1，则只能计算两个相机的内参数
对于方程Vb=0可以使用SVD求得其最小二乘解。对VTV进行SVD分解，其最小特征值对应的特征向量就是Vb=0的最小二乘解，从而求得矩阵B。由于这里得到的B的估计值是在相差一个常量因子下得到的，所以有：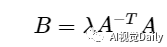
从而可以得到相机的各个内参数：

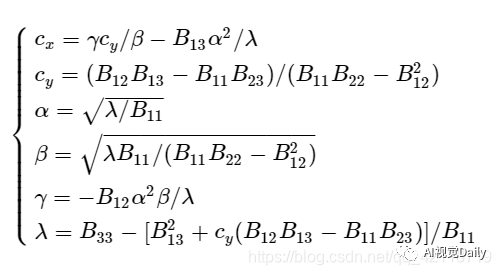
后面为了进一步增加标定结果的可靠性，可以使用最大似然估计(Maximum likelihood estimation)来优化上面估计得到的结果。
假设同一相机从n个不同的角度的得到了n幅标定板的图像，每幅图像上有m个像点。Mij表示第i幅图像上第j个像点对应的标定板上的三维点，则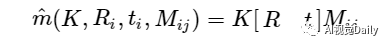
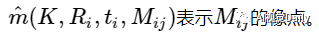
其中，Ri,ti表示第i幅图像对应相机的旋转矩阵和平移向量，K是相机的内参数。则像点mij的概率密度函数是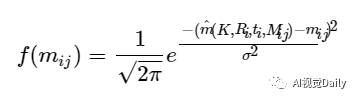
构造似然函数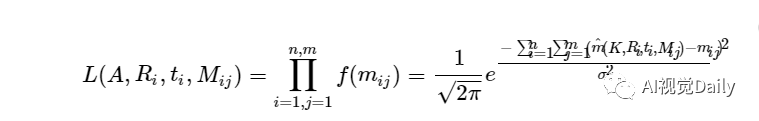
为了能够让L取得最大值，需要最小化下面的值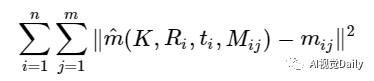

这是一个非线性优化问题，可以使用Levenberg-Marquardt的方法，利用上面得到的解作为初始值，迭代得到最优解。

如果您认可我的文章，希望能够关注我的微信公众号，我会不定期更新工作中学到的东西和一些技术比较前沿的东西。