网站制作一条龙/免费网站在线观看人数在哪

前言

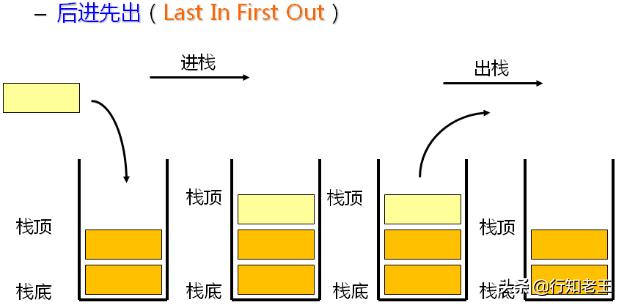
栈(stack)又称为堆栈或堆叠，栈作为一种数据结构，是一种只能在一端进行插入和删除操作的特殊线性表，也就是栈是一种操作受限的线性表。它按照先进后出的原则存储数据，先进入的数据被压入栈底，最后的数据在栈顶，需要读数据的时候从栈顶开始弹出数据(最后一个数据被第一个读出来)。栈具有记忆作用，对栈的插入与删除操作中，不需要改变栈底指针。

基本概念

栈是允许在同一端进行插入和删除操作的特殊线性表。允许进行插入和删除操作的一端称为栈顶(top)，另一端为栈底(bottom)；栈底固定，而栈顶浮动；栈中元素个数为零时称为空栈。插入一般称为进栈(PUSH)，删除则称为退栈(POP)。

由于堆叠数据结构只允许在一端进行操作，因而按照后进先出(LIFO, Last In First Out)的原理运作。栈也称为后进先出表。

生活中使用栈的场景很多，这里以羽毛球筒为例，羽毛球筒就是一个栈，刚开始羽毛球筒是空的，也就是空栈，然后我们一个一个放入羽毛球，也就是一个一个push进栈，当我们需要使用羽毛球的时候，从筒里面拿，也就是pop出栈，但是第一个拿到的羽毛球是我们最后放进去的。

与内存中栈的区别

• 内存中的堆栈和数据结构堆栈不是一个概念，可以说内存中的堆栈是真实存在的物理区，数据结构中的堆栈是抽象的数据存储结构。
• 内存空间在逻辑上分为三部分：代码区、静态数据区和动态数据区，动态数据区又分为栈区和堆区。
• 代码区：存储方法体的二进制代码。高级调度(作业调度)、中级调度(内存调度)、低级调度(进程调度)控制代码区执行代码的切换。
• 静态数据区：存储全局变量、静态变量、常量，常量包括final修饰的常量和String常量。系统自动分配和回收。
• 栈区：存储运行方法的形参、局部变量、返回值。由系统自动分配和回收。
• 堆区：new一个对象的引用或地址存储在栈区，指向该对象存储在堆区中的真实数据。

栈的实现

首先我们需要了解下栈都有哪些操作：

通过查看JDK中栈的源代码java.util.Stack，我们知道栈至少有下面几个操作：

• push 入栈
• pop 出栈
• peek 访问栈顶元素
• empty 判断栈是否为空
• search 查找站内元素

栈即可用数组实现，也可以用链表实现，用数组实现的栈，叫做顺序栈，用链表实现的栈，叫做链式栈。不管是顺序栈还是链式栈，入栈、出栈只涉及栈顶数据的操作，所以时间复杂度都是O(1)。

乞丐版(固定大小)

数组实现栈

//基于数组实现的顺序栈public class ArrayStack { private String[] items; // 数组 private int count; // 栈中元素个数 private int n; // 栈的大小 // 初始化数组，申请一个大小为 n 的数组空间 public ArrayStack(int n) { this.items = new String[n]; this.n = n; this.count = 0; } // 入栈操作 public boolean push(String item) { // 数组空间不够了，直接返回 false，入栈失败。 if (count == n) return false; // 将 item 放到下标为 count 的位置，并且 count 加一 items[count] = item; ++count; return true; } // 出栈操作 public String pop() { // 栈为空，则直接返回 null if (count == 0) return null; // 返回下标为 count-1 的数组元素，并且栈中元素个数 count 减一 String tmp = items[count - 1]; --count; return tmp; }}

链表实现栈

public static class LinkedListBasedStack { private int size; private Node top;  static Node createNode(String data, Node next) { return new Node(data, next); } public void clear() { this.top = null; this.size = 0; } public void push(String data) { Node node = createNode(data, this.top); this.top = node; this.size++; } public String pop() { Node popNode = this.top; if (popNode == null) { System.out.println("Stack is empty."); return null; } this.top = popNode.next; if (this.size > 0) { this.size--; } return popNode.data; } public String getTopData() { if (this.top == null) { return null; } return this.top.data; } public int size() { return this.size; } public void print() { System.out.println("Print stack:"); Node currentNode = this.top; while (currentNode != null) { String data = currentNode.getData(); System.out.print(data + ""); currentNode = currentNode.next; } System.out.println(); } public static class Node { private String data; private Node next; public Node(String data) { this(data, null); } public Node(String data, Node next) { this.data = data; this.next = next; } public void setData(String data) { this.data = data; } public String getData() { return this.data; } public void setNext(Node next) { this.next = next; } public Node getNext() { return this.next; } }}

增强版(动态扩容)

上面我们实现的栈，都是固定大小的，也就是说，在初始化栈时需要制定栈的大小，而且一旦初始化，后边是不能扩容的，当栈满了以后，就不能再往栈里添加数据了。尽管链式栈的大小不受限，但是需要存储指针，内存消耗会比较多。

在学习数组的时候，我们实现了一个支持动态扩容的数组，就是当数组空间不够用时，重新申请一块更大的内存，将原来数组汇总的数据拷贝进去，这样就实现了一个支持动态扩容的数组。同理，动态扩容的栈也可以这样做，当栈满了以后，就申请一个更大的数组将原来的数据搬移到新的数据中，我们可以看下JDK源码中对栈进行扩容的部分：

/** * This implements the unsynchronized semantics of ensureCapacity. * Synchronized methods in this class can internally call this * method for ensuring capacity without incurring the cost of an * extra synchronization. * * @see #ensureCapacity(int) */private void ensureCapacityHelper(int minCapacity) { // overflow-conscious code if (minCapacity - elementData.length > 0) grow(minCapacity);}/** * The maximum size of array to allocate. * Some VMs reserve some header words in an array. * Attempts to allocate larger arrays may result in * OutOfMemoryError: Requested array size exceeds VM limit */private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;private void grow(int minCapacity) { // overflow-conscious code int oldCapacity = elementData.length; int newCapacity = oldCapacity + ((capacityIncrement > 0) ? capacityIncrement : oldCapacity); if (newCapacity - minCapacity < 0) newCapacity = minCapacity; if (newCapacity - MAX_ARRAY_SIZE > 0) newCapacity = hugeCapacity(minCapacity); elementData = Arrays.copyOf(elementData, newCapacity);}private static int hugeCapacity(int minCapacity) { if (minCapacity < 0) // overflow throw new OutOfMemoryError(); return (minCapacity > MAX_ARRAY_SIZE) ? Integer.MAX_VALUE : MAX_ARRAY_SIZE;}

是不是很熟悉，链表就是这么干的，其实底层都是用的数组拷贝。现在我们已经知道如何实现一个动态扩容的栈了：

import java.util.Arrays;import java.util.EmptyStackException;public class ArrayBasedStackUp { // 存储元素的数组,声明为Object类型能存储任意类型的数据 private Object[] elementData; // 指向栈顶的指针 private int top; // 栈的总容量 private int size; // 默认构造一个容量为10的栈 public ArrayBasedStackUp() { this.elementData = new Object[10]; this.top = -1; this.size = 10; } public ArrayBasedStackUp(int initialCapacity) { if (initialCapacity < 0) { throw new IllegalArgumentException("栈初始容量不能小于0: " + initialCapacity); } this.elementData = new Object[initialCapacity]; this.top = -1; this.size = initialCapacity; } // 压入元素 public Object push(Object item) { // 是否需要扩容 isGrow(top + 1); elementData[++top] = item; return item; } // 弹出栈顶元素 public Object pop() { Object obj = peek(); remove(top); return obj; } // 获取栈顶元素 public Object peek() { if (top == -1) { throw new EmptyStackException(); } return elementData[top]; } // 判断栈是否为空 public boolean isEmpty() { return (top == -1); } // 删除栈顶元素 public void remove(int top) { // 栈顶元素置为null elementData[top] = null; this.top--; } /** * 是否需要扩容，如果需要，则扩大一倍并返回true，不需要则返回false *  * @param minCapacity * @return */ public boolean isGrow(int minCapacity) { int oldCapacity = size; // 如果当前元素压入栈之后总容量大于前面定义的容量，则需要扩容 if (minCapacity >= oldCapacity) { // 定义扩大之后栈的总容量 int newCapacity = 0; // 栈容量扩大两倍(左移一位)看是否超过int类型所表示的最大范围 if ((oldCapacity << 1) - Integer.MAX_VALUE > 0) { newCapacity = Integer.MAX_VALUE; } else { newCapacity = (oldCapacity << 1);// 左移一位，相当于*2 } this.size = newCapacity; elementData = Arrays.copyOf(elementData, size); return true; } else { return false; } }}

我们来分析下支持动态扩容的顺序栈的入栈、出栈操作的时间复杂度。对于出栈操作来说，不会涉及内存的重新申请和数据的搬移，所以时间复杂度还是O(1)，但是，对于入栈来说就不一样了，当栈中有空余空间时，入栈的操作时间复杂度就是O(1)，但是当空间不够时，就需要重新申请内存和数据搬移，时间复杂度就成了O(n)。因为只有极少数情况才会进行数据搬移(只有栈满才会搬移)，少数服从多数，所以平均时间复杂度就是O(1)。

栈的应用

函数调用栈

函数调用栈是非常经典的应用场景，我们知道，操作系统给每个线程分配了一块独立的内存空间，这块内存空间被组织成栈这种结构，用来存储函数调用时的临时变量，每进入一个函数，会将临时变量作为一个栈帧入栈，函数调用完成后，将这个函数对应的栈帧出栈。来看下边这段代码：

public static void main(String[] args) { int a = 1; int ret = 0; int res = 0; ret = add(3, 5); res = a + ret; System.out.println(res);}public static int add(int x, int y) { int sum = 0; sum = x + y; return sum;}

main函数调用add函数，获取到add函数的计算结果，并且与临时变量a相加，然后打印res的值。下图是执行到add函数时，函数调用栈的使用情况：

为什么函数调用要用“栈”来保存临时变量呢？用其他数据结构不行吗？

其实，我们不一定非要用栈来保存临时变量，只不过如果这个函数调用符合后进先出的特性，用栈这种数据结构来实现，是最顺理成章的选择。

从调用函数进入被调用函数，对于数据来说，变化的是什么呢？是作用域。所以根本上，只要能保证每进入一个新的函数，都是一个新的作用域就可以。而要实现这个，用栈就非常方便。在进入被调用函数的时候，分配一段栈空间给这个函数的变量，在函数结束的时候，将栈顶复位，正好回到调用函数的作用域内。

表达式求值

20世纪50年代，波兰逻辑学家Jan Łukasiewicz想到了一种不需要括号的后缀表达法，即逆波兰(Reverse Polish Notation)表示，这一表示方式，巧妙地解决了程序实现四则运算的难题。

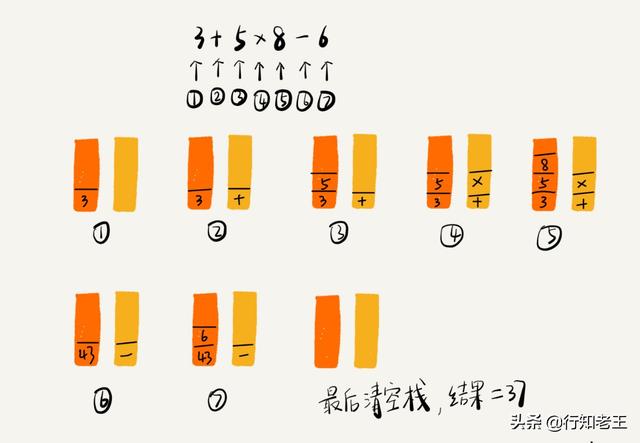
在计算机中，表达式求值是利用两个栈来实现的，一个栈保存操作数，一个栈保存运算符，我们从左到右遍历表达式，当遇到数字时，就直接压入操作数栈，当遇到运算符时，就与运算符栈的栈顶元素进行比较，如果比运算符栈的栈顶元素优先级高，就将当前运算符压入栈，如果比运算符栈的栈顶元素优先级相同，从运算符栈中取出栈顶运算符，从操作数栈中取栈顶两个操作数，然后进行计算，再把计算的结果压入操作数栈，继续比较。

我们以3+5*8-6为例，理解下上面的过程：

import java.util.Scanner;import java.util.Stack;/** * 程序代码来源于：https://blog.csdn.net/guying_2016/article/details/82348464 * 思路参考：https://blog.csdn.net/u011446177/article/details/42389511?locationNum=15&fps=1 * 四则运算的两个操作过程及其他辅助判断 *  * 使用栈实现四则运算 * 1.中缀表达式 --> 后缀表达式  * 思路：从左到右遍历中缀表达式的每个数字和符号  * 若是数字，直接输出(或保存到某一链表中) * 若是符号，则判断其与栈顶符号的优先级 是 右括号 或 优先级不高于 栈顶符号的优先级，则栈顶元素依次出栈并输出 并将当前符号进栈，一直到最终输出后缀表达式为止。 * 注意：栈顶元素与当前符号优先级相同也要输出！ * 2.后缀表达式进行四则运算 * 思路：把数字压入堆栈，遇到操作符就从栈中取出两个数进行相关运算，把结果在存放入栈中直到最后操作完成，输出最终结果 */public class ArithmeticExp { // 成员变量 private String prefixExp; // 前缀表达式 private String infixExp; // 中缀表达式 private String postfixExp; // 后缀表达式 /** * 构造方法 */ public ArithmeticExp() { } public ArithmeticExp(String infixExp) { this.infixExp = infixExp; } public String getPrefixExp() { return prefixExp; } public void setPrefixExp(String prefixExp) { this.prefixExp = prefixExp; } public String getInfixExp() { return infixExp; } public void setInfixExp(String infixExp) { this.infixExp = infixExp; } public String getPostfixExp() { return postfixExp; } public void setPostfixExp(String postfixExp) { this.postfixExp = postfixExp; } /** * 1.转化成后缀表达式(逆波兰表达式) */ public void cover2PostfixExp() { // 创建堆栈 Stack ls = new Stack(); this.postfixExp = ""; // 遍历表达式的每一个字符 for (int i = 0; this.infixExp != null && i < this.infixExp.length(); i++) { char ch = this.infixExp.charAt(i); if (' ' != ch) { // 当前字符不为空 时的操作 if (isLeftBracket(ch)) { // 是左括号，压栈 ls.push(ch); } else if (isRightBracket(ch)) { // 是右括号，将所有操作符出栈，直到遇到一个左括号，并将这个左括号丢弃 char topOperator = ls.pop(); while (!isLeftBracket(topOperator)) { postfixExp += (topOperator + " "); // 使用空格 隔开 topOperator = ls.pop(); } } else if (isOperator(ch)) { // 是操作符，要判断优先级，再决定是否需要入栈 /** * 如果栈为空，直接进栈。如果栈非空，则需要将栈顶运算符的优先级和要入栈的运算符的优先级进行比较 * 将栈中比要入栈的运算符优先级高的运算符都出栈，然后将该运算符入栈 */ if (!ls.isEmpty()) { // 如果栈非空 // 获取栈顶的运算符 Character topOperator = ls.peek(); while (topOperator != null && priority(topOperator.charValue()) >= priority(ch)) { postfixExp += (ls.pop() + " "); if (!ls.isEmpty()) { topOperator = ls.peek(); } else { break; } } } // 将当前操作符 压栈 ls.push(ch); } else { if (i > 0 && isNumber(infixExp.charAt(i - 1))) { postfixExp = postfixExp.substring(0, postfixExp.length() - 1) + ch + " "; } else { postfixExp += ch + " "; } } } } while (!ls.isEmpty()) { postfixExp += (ls.pop() + " "); } // 去除表达式中的最后一个空格 // postfixExp = postfixExp.substring(0, postfixExp.length() - 1); postfixExp = postfixExp.trim(); } /** * 运算符优先级比较 *  * @param charValue * @return */ public int priority(char charValue) { switch (charValue) { case '+': case '-': return 1; case '*': case '/': case '%': return 2; case '^': return 3; } return 0; } /** * 判断是否是操作符 *  * @param ch * @return */ public boolean isOperator(char ch) { if (ch == '+' || ch == '-' || ch == '*' || ch == '/' || ch == '^' || ch == '%') { return true; } return false; } /** * 2.使用后缀表达式 进行 四则运算 */ public int calculateExpResult() { String[] strs = this.postfixExp.split(" "); Stack ls = new Stack(); for (int i = 0; i < strs.length; i++) { // 如果是操作符，从堆栈获取两个值，进行运算 if (strs[i].length() == 1 && isOperator(strs[i].charAt(0))) { int num2 = ls.pop(); int num1 = ls.pop(); ls.push(calculate2Numbers(num1, num2, strs[i].charAt(0))); } else { // 如果是数字，压入堆栈 ls.push(Integer.parseInt(strs[i])); } } return ls.pop(); } /** * 两数的运算操作 *  * @param num1 * @param num2 * @param operator * @return */ public Integer calculate2Numbers(int num1, int num2, char operator) { switch (operator) { case '+': return num1 + num2; case '-': return num1 - num2; case '*': return num1 * num2; case '/': return num1 / num2; case '%': return num1 % num2; case '^': return num1 ^ num2; } return null; } /** * 判断是否是左括号 *  * @param ch * @return 布尔值 */ public boolean isLeftBracket(char ch) { if (ch == '(') { return true; } return false; } /** * 判断是否是右括号 *  * @param ch * @return 布尔值 */ public boolean isRightBracket(char ch) { if (ch == ')') { return true; } return false; } /** * 判断是否是数字 *  * @param ch * @return */ public boolean isNumber(char ch) { if (ch >= '0' && ch <= '9') { return true; } return false; } // 中缀表达式：9+(3-1)*3+10/2 public static void main(String[] args) { // 从控制台获取中缀表达式 Scanner sc = new Scanner(System.in); String infixExp = sc.nextLine(); sc.close(); // 创建对象，进行后续操作 ArithmeticExp ae = new ArithmeticExp(infixExp); System.out.println("中缀表达式：" + ae.getInfixExp()); // 转化为后缀表达式 ae.cover2PostfixExp(); System.out.println("后缀表达式：" + ae.getPostfixExp()); System.out.println(ae.getPostfixExp().length()); // 使用后缀表达式 进行 四则运算 int calculateExpResult = ae.calculateExpResult(); // 结果输出 System.out.println("计算结果：" + calculateExpResult); }}

栈实现字符串逆序

我们知道栈是后进先出，我们可以将一个字符串分隔为单个的字符，然后将字符一个一个push()进栈，在一个一个pop()出栈就是逆序显示了。如下：

// 利用栈反转字符串public void testStringReversal() { ArrayBasedStackUp stack = new ArrayBasedStackUp(); String str = "how are you"; char[] cha = str.toCharArray(); for (char c : cha) { stack.push(c); } while (!stack.isEmpty()) { System.out.print(stack.pop()); }}

判断括号匹配

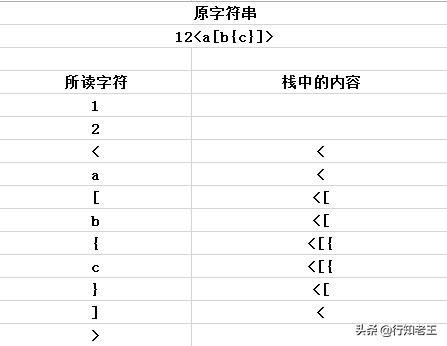
写XML或者HTML标签时，括号都是成对出现的，比如就是匹配的一对，对于 12，我们可以将字符一次入栈，遇到匹配正确的就消除，最后栈中的内容为空则匹配成功，否则匹配失败。如下图所示：

// 利用栈判断括号是否匹配public void testMatch() { ArrayBasedStackUp stack = new ArrayBasedStackUp(3); String str = "12"; char[] cha = str.toCharArray(); for (char c : cha) { switch (c) { case '{': case '[': case '': if (!stack.isEmpty()) { char ch = stack.pop().toString().toCharArray()[0]; if (c == '}' && ch != '{' || c == ']' && ch != '[' || c == ')' && ch != '(') { System.out.println("Error:" + ch + "-" + c); } } break; default: break; } }}

栈实现浏览器前进后退

实现浏览器的前进后退功能，需要用两个栈，栈X和栈Y，我们把首次浏览的页面依次加入栈X，当点击后退按钮时，再依次从栈X中出栈，将出栈的数据依次放入栈Y，当按前进按钮时，依次从栈Y中取出数据，放入栈X中，当栈X中没有数据时，说明没有页面可以进行后退了，当Y中没有数据时，说明没有页面可以前进浏览了。如果在回退浏览的过程中，跳入了栈中不存在的页面，这时候就要清空栈Y中的数据。

public class SampleBrowser { public static void main(String[] args) { SampleBrowser browser = new SampleBrowser(); browser.open("http://www.baidu.com"); browser.open("http://news.baidu.com/"); browser.open("http://news.baidu.com/ent"); browser.goBack(); browser.goBack(); browser.goForward(); browser.open("http://www.qq.com"); browser.goForward(); browser.goBack(); browser.goForward(); browser.goBack(); browser.goBack(); browser.goBack(); browser.goBack(); browser.checkCurrentPage(); } private String currentPage; private LinkedListBasedStack backStack; private LinkedListBasedStack forwardStack; public SampleBrowser() { this.backStack = new LinkedListBasedStack(); this.forwardStack = new LinkedListBasedStack(); } public void open(String url) { if (this.currentPage != null) { this.backStack.push(this.currentPage); this.forwardStack.clear(); } showUrl(url, "Open"); } public boolean canGoBack() { return this.backStack.size() > 0; } public boolean canGoForward() { return this.forwardStack.size() > 0; } public String goBack() { if (this.canGoBack()) { this.forwardStack.push(this.currentPage); String backUrl = this.backStack.pop(); showUrl(backUrl, "Back"); return backUrl; } System.out.println("* Cannot go back, no pages behind."); return null; } public String goForward() { if (this.canGoForward()) { this.backStack.push(this.currentPage); String forwardUrl = this.forwardStack.pop(); showUrl(forwardUrl, "Foward"); return forwardUrl; } System.out.println("** Cannot go forward, no pages ahead."); return null; } public void showUrl(String url, String prefix) { this.currentPage = url; System.out.println(prefix + " page == " + url); } public void checkCurrentPage() { System.out.println("Current page is: " + this.currentPage); }}

微信公众号：行知老王