如何快速建设推广网站/seo学习

Description
给出一个n个点的无向图，求所有子图的最小染色数
Input
第一行为一整数T表示用例组数，每组用例首先输入点数n，之后一个n*n的01矩阵表示该无向图的邻接矩阵(1<=T<=100,1<=n<=18)
Output
输出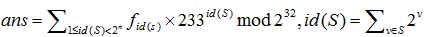，f表示S的最小染色
Sample Input
2
4
0110
1010
1101
0010
4
0111
1010
1101
1010
Sample Output
1022423354
2538351020
Solution
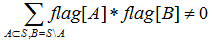
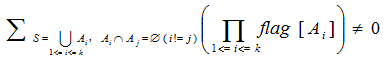
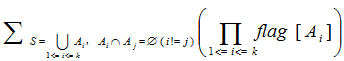
用一个n位的二进制数表示一个点集的诱导子图，用O(n*2^n)可以得到所有最小独立集，用flag[i]表示i这个子图是否是独立集，若flag[i]=1说明i是独立集，那么其最小染色就是1，下面处理flag[i]=0的子图，对于S这个点集，若其不是一个独立集且有，说明至少存在一个S的子集A，使得A和B都是独立集（B=S\A），进而S的最小染色就是2；然后按以上步骤以此求3-染色子图，4-染色子图，……；对于点集S，若其不是1-染色，2-染色，……k-1-染色子图，且有，那么说明至少存在一种方案使得S可以表示为k个无交独立集的并，且S不能表示为较少的无交独立集的并，故S的最小染色就是k。这样做n遍就可以得到所有染色的子图，所以问题变成如何求上面提到的卷积，这里就要用到FWT（快速威尔式变换）了，具体过程就是首先对flag[i]做一遍高维前缀和，之后把flag[i]做k次方后再做一遍高位前缀差，若某个flag[i]不为0说明i这个点集的最小染色就是k，总时间复杂度就是O(n^2*2^n)
Code

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
#define mod 4294967296
#define maxn (1<<19)
ll f[maxn],sum[maxn];
int T,n,g[22],vis[maxn],flag[maxn];
char s[22];
void init()
{f[0]=1;for(int i=1;i<(1<<18);i++)f[i]=233ll*f[i-1]%mod;
}
bool check(int x)
{if(x==0)return 0;for(int i=0;i<n;i++)if(x&(1<<i))if(x&g[i])return 0;return 1;
}
int main()
{init();scanf("%d",&T);while(T--){memset(vis,0,sizeof(vis));scanf("%d",&n);for(int i=0;i<n;i++){g[i]=0;scanf("%s",s);for(int j=0;j<n;j++)g[i]+=(s[j]-'0')<<j;}int sta=1<<n;ll ans=0;for(int i=0;i<sta;i++){if(check(i))flag[i]=1,vis[i]=1,ans=(ans+f[i])%mod;else flag[i]=0;}for(int i=0;i<sta;i++)sum[i]=flag[i];for(int i=0;i<n;i++)for(int j=0;j<sta;j++)if(j&(1<<i))flag[j]+=flag[j^(1<<i)];for(int k=2;k<=n;k++){       for(int i=0;i<n;i++)for(int j=0;j<sta;j++)if(j&(1<<i))sum[j]+=sum[j^(1<<i)];for(int i=0;i<sta;i++)sum[i]*=flag[i];for(int i=0;i<n;i++)for(int j=0;j<sta;j++)if(j&(1<<i))sum[j]-=sum[j^(1<<i)];for(int i=0;i<sta;i++)if(sum[i]!=0&&!vis[i])vis[i]=1,ans=(ans+1ll*k*f[i]%mod)%mod;}printf("%I64d\n",ans%mod);}return 0;
}