黄山网站设计/免费个人主页网站

　　前言

　　在前面的博文PCA算法学习_1(OpenCV中PCA实现人脸降维)中已经初步介绍了PCA算法的大概流程及在人脸降维上面的应用。本文就进一步介绍下其理论基础和matlab的实现（也是网上学者的代码）。

　　开发环境：Matlab2012a

 

　　基础

主成分分析(PrincipalComponents Analysis。即PCA，也称为K-L变换)，是图像压缩中的一种最优正交变换。PCA用于统计特征提取构成了子空间法模式识别的基础。它从图像整体代数特征出发，基于图像的总体信息进行分类识别。PCA的核心思想是利用较少数量的特征对样本进行描述以达到降低特征空间维数的目的。

1.  PCA理论

给定一副N*N大小图像，将它表示成一个N²*1维向量，向量中元素为像素点灰度，按行存储，如下列公式分别表示第i张图片和n张图片平均值：

令N²*1矩阵X为：

注意，矩阵减去平均值相当于将坐标系原点移动到平均值位置。

设Q=XX^T，则Q是一个N²* N²矩阵：

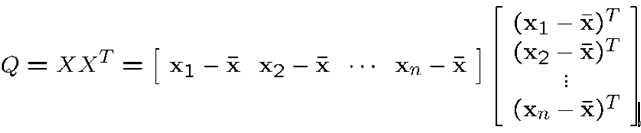
,Q是方阵

,Q是对称矩阵。

,Q被成为协方差矩阵，

,Q的数据量非常庞大

    那么，X中的每个元素x_j可以被如下表达：

其中,e_i是Q中非零特征值对应的特征向量。由特征向量e₁,e₂,…,e_n组成的空间叫做张成的特征空间。对于N*N图像，e₁,e₂,…,e_n是N²*1维相互正交的向量。尺度g_ji是x_j在空间中的坐标。

为了降维，可以对特征值设定阈值或按照其他准则，寻找协方差矩阵Q中前k个特征向量。这里Q十分庞大，对于一副256*256的图像，Q的大小为65536*65536！替代方案是，考虑矩阵

.P和Q都是对称矩阵

.P≠Q^T

.Q的大小是N²*N²，而P大小为n*n

.n为训练样本图像数量，通常n<<N

　源码
　假设X是一个m*n的矩阵，是由样本数据构成的矩阵。其中m表示样本的属性维数，n表示样本的个数。现在要对X进行线性变换变成另一个矩阵Y，使得Y的协方差矩阵为对角矩阵，这样的Y就认为是对原始矩阵X提取主成分后的矩阵，实际过程中只需取Y的前面主要的行即可。

　　X变换到Y的线性变换公式为:

　　

　　X和Y的协方差计算方法为：

　　

　　

　　从下面的公式可以看出Cy和Cx的关系为：

　　

　　因为Cx是对称矩阵，对Cx进行特征值分解就可以将其变换成对角矩阵，见下面的公式推导：

 　　

　　公式中的P和E满足：

 　　

　　其中D是由Cx的特征向量构成的对角矩阵。P是线性变换矩阵，P的每一行都是Cx矩阵的特征向量，且P是正交矩阵，一般情况下把特征值大的特征向量排在矩阵前面几行。

　　由此可知，求出P后就可以求出X主成分矩阵了。

　　另外，还可以求出PCA的白化矩阵，PCA的白化矩阵就是特征向量去相关的矩阵，白化矩阵的协方差阵一般为单位矩阵，在PCA中可以这么求：inv(sqrt(D))*E'。普通的PCA算法可以将输入矩阵X变成主成分矩阵Y，尽管Y的协方差矩阵是个对角矩阵，但不一定是单位矩阵，如果对Y继续使用白化操作，则Y的协方差矩阵就变成了单位矩阵了。

 

　　该pca函数接口形式为：

[Y,V,E,D] = pca(X)

　　其中X为输入数据，X的每一列是一个输入样本。返回值Y是对X进行PCA分析后的投影矩阵。V是与X有关的协方差矩阵特征向量的白化矩阵，E是对应的特征向量（列）构成的矩阵，D是对应的特征值构成的对角矩阵（特征值处于对角线上）。返回值中的白化矩阵，特征向量和特征值都是按照对应特征值大小进行排序后了的。

　　其matlab源码如下：

function [Y,V,E,D] = pca(X)% do PCA on image patches
%
% INPUT variables:
% X                  matrix with image patches as columns
%
% OUTPUT variables:
% Y                  the project matrix of the input data X without whiting
% V                  whitening matrix
% E                  principal component transformation (orthogonal)
% D                  variances of the principal components%去除直流成分
X = X-ones(size(X,1),1)*mean(X);% Calculate the eigenvalues and eigenvectors of the new covariance matrix.
covarianceMatrix = X*X'/size(X,2); %求出其协方差矩阵
%E是特征向量构成，它的每一列是特征向量，D是特征值构成的对角矩阵
%这些特征值和特征向量都没有经过排序
[E, D] = eig(covarianceMatrix); % Sort the eigenvalues  and recompute matrices
% 因为sort函数是升序排列，而需要的是降序排列，所以先取负号,diag(a)是取出a的对角元素构成
% 一个列向量，这里的dummy是降序排列后的向量，order是其排列顺序
[dummy,order] = sort(diag(-D));
E = E(:,order);%将特征向量按照特征值大小进行降序排列，每一列是一个特征向量
Y = E'*X;
d = diag(D); %d是一个列向量
%dsqrtinv是列向量，特征值开根号后取倒,仍然是与特征值有关的列向量
%其实就是求开根号后的逆矩阵
dsqrtinv = real(d.^(-0.5)); 
Dsqrtinv = diag(dsqrtinv(order));%是一个对角矩阵，矩阵中的元素时按降序排列好了的特征值（经过取根号倒后）
D = diag(d(order));%D是一个对角矩阵，其对角元素由特征值从大到小构成
V = Dsqrtinv*E';%特征值矩阵乘以特征向量矩阵