继续上一篇笔记，本文接着讲 堆 。

堆

堆是一类完全二叉树，常用于实现排序，选择最小（大）值和优先队列等

**优先队列：**一种特殊的队列，队列中元素出栈的顺序是按照元素的优先权大小，而不是元素入队的先后顺序。

堆的定义

堆通常是一个可以被看做一棵树的数组对象。堆总是满足下列性质：

• 堆中所有非叶子结点总是不大于或不小于其左右孩子结点
• 堆总是一棵完全二叉树

即按完全二叉树的结点编号排列，n个结点的关键字序列称为堆。

堆可分为：

• 小顶堆：若堆中所有非叶子结点均不大于其左右孩子结点，则称为小顶堆，显然，根节点必为 n 个结点的最小值
• 大顶堆：若堆中所有非叶子结点均不小于其左右孩子结点，则称为大顶堆，显然，根节点必为 n 个结点的最大值

相关概念：

• 子堆：堆中的子树称为子堆
• 堆顶：堆中根节点的位置称为堆顶
• 堆尾：堆中最后结点的位置称为堆尾
• 堆长度：堆中结点的个数称为堆长度

堆的存储结构类型与完全二叉树有所不同，定义如下：

typdefstruct {RcdType *rcd;	//堆基址，0号单元闲置int n;			//堆长度int size;		//堆容量int tag; 		//小顶堆与大顶堆的标志：tag = 0为小顶堆，tag = 1为大顶堆int (* prior)(KeyType,KeyType); //函数变量，用于关键字优先级比较
} Heap;				//堆类型
/* 假设关键字类型为整型，大顶堆和小顶堆的优先函数可分别定义如下： */
int greatPrior(int x,int y)	{	return x>=y;	}
int lessPrior(int x,int y)	{	return x<=y;	}

堆的实现

堆的筛选

堆的筛选：将堆中指定的以 pos 结点为根的子树调整为子树，其前提是 pos 结点的左右子树均为子堆。

筛选操作的过程：

• 将 pos 结点与左右孩子较优先者比较，若 pos 结点较优先则结束
• 否则 pos 结点与左右孩子中较优先者交换位置，pos 位标下移
• 重复上述步骤，直至 pos 指示叶子节点

算法如下：

Status swapHeapElem(Heap &H, int i, int j){//交换堆H中的第i结点和第j结点RcdType temp;if(i<=0 || i>H.n || j<=0 || j>H.n) {return ERROR;}temp = H.rcd[i];H.rcd[i] = H.rcd[j];H.rcd[j] = temp;return OK;
}
void ShiftDown(Heap &H, int pos) {//对堆H中位置为 pos 的结点做筛选，将以 pos 为根的子树调整为子堆int lc,rc;while(pos<=H.n/2) { //若pos结点为叶子结点，循环结束lc = pos*2;     //lc为pos结点的左孩子位置rc = pos*2+1；  //rc为pos结点的右孩子位置if(rc<=H.n&&H.prior(H.rcd[rc].key,H.rcd[lc].key)){   lc = rc;    //lc为pos结点的左右孩子中较优先者的位置}if(H.prior(H.rcd[pos].key,H.rcd[lc].key)){return;     //若pos结点较优先，则筛选结束}swapHeapElem(H, pos, lc); //否则pos和较优先者lc交换位置pos = lc;				  //继续向下调整}
}

该筛选算法的时间复杂度为O(logn)

堆的插入

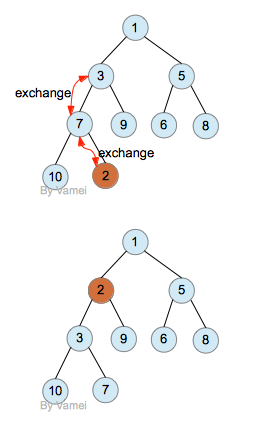
插入操作：将插入元素加到堆尾，此时须判别堆尾和其双亲结点是否满足堆特性，若不满足，则需要进行向上调整，将插入元素与双亲交换；交换后，插入元素若存在双亲且此双亲结点不满足堆特性，则需要继续重复上述过程。

步骤：

• 将插入元素加到堆尾，并用 curr 指示堆尾
• 若 curr 指示堆尾，插入操作结束，否则，将 curr 结点与其双亲结点比较，若 curr 结点较优先则交换， curr 上移，重复本步骤；否则操作结束

算法如下：

Status InsertHeap(Heap &H, RcdType e) {//将结点 e 插入至堆H中int curr;if(H.n>=H.size-1)	return ERROR; //堆已满，插入失败curr = ++H.n;H.rcd[curr] = e; //将插入元素加到堆尾while(1!=curr && H.prior(H.rcd[curr].key,H.rcd[curr/2].key)){swapHeapElem(H, curr, curr/2); //交换curr与curr/2结点，向上调整curr /=2;}return OK;
}

该插入算法的时间复杂度为O(logn)。

筛选与插入区别：

• 筛选操作是叶子节点向上调整；
• 插入操作是叶子节点向下调整

建堆

• 单节点的完全二叉树满足堆特性，叶子结点都是堆
• n 个结点的完全二叉树建堆，须将以编号为n/2、n/2-1、…、1的结点为根的子树筛选为子堆

算法如下:

void MakeHeap(Heap &H, RcdType *E, int n, int size, int tag,int (* prior)(KeyType,KeyType)) {//prior 为自定义的优先函数int i;//初始化H.rcd = E;H.n = n; H.size = size; H.tag = tag; H.prior = prior;//对以i结点为根的子树进行筛选for(i=n/2; i>0; i--) {ShiftDown(H, i);}
}

该建堆算法的时间复杂度为O(n)。

删除堆顶结点

操作：删除堆顶结点后，需对新的堆顶结点进行筛选

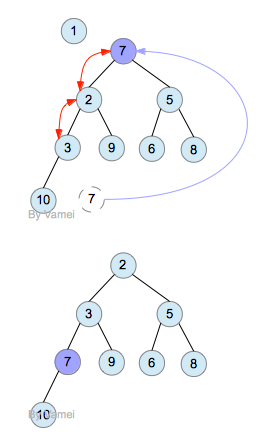
算法如下：

Status RemoveFirstHeap(Heap &H, RcdType &e) {//删除堆H的堆顶结点，并用e返回if(H.n<=0)	return ERROR; //堆已满，插入失败e =H.rcd[1]; 			  //取堆顶结点swapHeapElem(H, 1, H.n);  //交换堆顶与堆尾结点，H.n--;					  //堆长度减1if(H.n>1) ShiftDown(H, 1);//对新的堆顶结点进行筛选return OK;
}

堆排序

堆排序属于选择类排序。

选择类排序的基本思想：在 n 个记录中，第 i 趟（i = 1,2,…,n-1）在第 i 到 n 个记录中选取关键字最小的记录作为有序序列中的第 i 个记录。选取最小关键字的策略决定了选择类排序算法的效率。

堆排序可采用大顶堆进行升序排序，采用小顶堆进行降序排序。

以大顶堆升序排序为例

• 先将待排序列建成大顶堆
• 将堆顶与堆尾交换位置（也就是删除堆顶结点操作），堆长度-1，取堆顶结点进新序列
• 对新的堆顶结点进行筛选，得到次大值结点
• 重复以上步骤，可得一个升序序列

算法如下：

void HeapSort(RcdSqList &L) {//L为待排序列Heap H; RcdType e; int i;//将待排序列建成大顶堆MakeHeap(H, L.rcd, L.length, L.size, 1, greatPrior);//对以i结点为根的子树进行筛选for(i=H.n; i>0; i--) {//交换堆顶与堆尾结点，堆长度减1，筛选新的堆顶结点RemoveFirstHeap(H, e);}
}

堆排序算法的时间复杂度最坏为O(nlogn)，空间复杂度为O(1)。

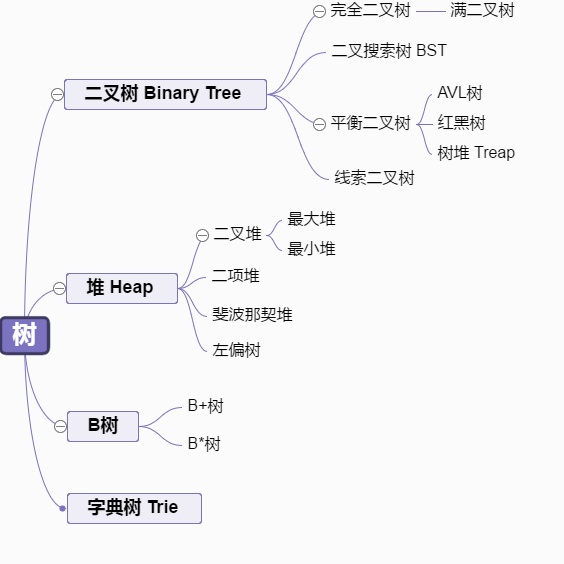
附上一张总结图