萍乡公司做网站/sem推广竞价托管

一.基础知识
1.查找——线性结构——折半查找/二分查找
2.适用：有序+顺序表
3.初始low指向第一个，high指向最后一个

二.查找过程及代码

1.查找成功

int low=0,high=L.TableLen-1,mid;

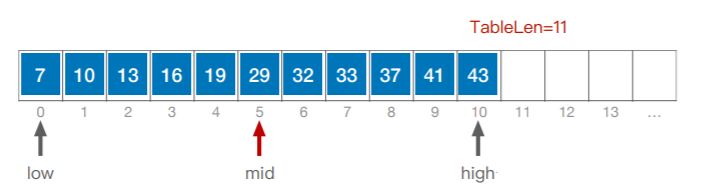
mid=(low+high)/2;

奇数个mid指向中间，偶数个mid指向中间左边的（向下取整）

查找33，29<33

if(L.elem[mid]<key);//key为要查找的33

在mid=29右侧，即处在(29,43]之间
移动low至mid右侧：6号位的32

low=mid+1;

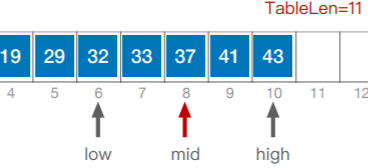
此时mid=37,37>33
移动high至mid左侧：7号位的33

if(L.elem[mid]>key) high=mid-1;

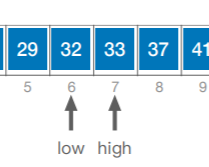
mid指向左边，即6号位的32

要查找的33>32，要右侧，即low移到mid右侧：7号位的33

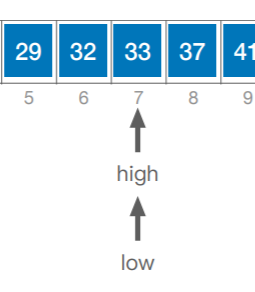
此时就剩一个33，mid指向，匹配成功
此时：low=high=mid
查找成功

if(L.elem[mid]==key)return mid;

2.查找失败

查找12







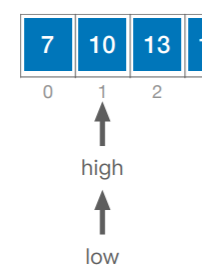
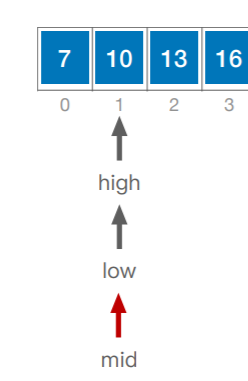
此时仍然没有匹配到，查找的12>10，取右侧，low移到mid+1
停止，查找失败，low>high

low>high;//程序结束，查找失败
//在查找过程中可以通过while(low<=high)让程序执行

通过-1返回

return -1;

3.完整代码

int Binary_Search(SeqList L, ElemType key) {int low = 0, high = L.length - 1, mid;while (low <= high) {mid = (low + high) / 2;if (L.elem[mid] == key)return mid;else if (L.elem[mid] > key)high = mid - 1;elselow = mid + 1;}return -1;
}

三.效率分析：判定树及ASL

1.判定树：mid掰

方框下的数字表示数组下标

每次取中间，两个中间取左边（向下取整）
mid=(low+high)/2向下取整


可以看到，
正常情况：左右掰下去，两边都有；
特殊情况：取左，右边掰到右子树
总结：
（1）右子树至多比左子树多一个元素。即：对于任意一个结点，必有右子树结点数-左子树结点数=0或1
（2）折半查找的判定树中，只有最下面一层可能不满
（3）折半查找的判定树一定是平衡二叉树，也满足二叉排序树的定义
（4）元素个数为n是树高h=log₂(n+1)向上取整（h不包括失败结点）
（5）特殊：如果对于偶数每次取右侧，即mid=(low+high)/2向上取整，在判定树中变为固定右侧，左侧下落，即左侧子树至多比右侧子树多一个元素

查找失败紫色补全：每个绿色结点的度都要补全

从图中可以看到，
绿色结点数目为n，一个结点2个度。度上接一个新节点占用一个度又产生2个度，即增加一个结点多一个度，即：紫色个数为2（初始结点提供的两个度）+n-1（后面n-1个结点每个占用1个提供2个）=n+1
即：失败结点个数n+1个

按照上面的规则，判定树的构造顺序（按序号顺序依次构造）

2.求ASL

ASL_成功=（11+22+34+44）/11=3
ASL_失败=(34+48)/12=11/3

因此，不论是查找成功还是失败，比较次数均不超过树高h=log₂(n+1)向上取整
故折半查找的时间复杂度O(log₂n)