目录

1.栈的介绍

2.栈的模拟实现

3.栈的基本用法

4.部分栈有关oj解析

---

1.栈的介绍

栈作为一种数据结构，是一种只能在一端进行插入和删除操作的特殊线性表。它按照先进后出的原则存储数据，先进入的数据被压入栈底，最后的数据在栈顶，需要读数据的时候从栈顶开始弹出数据（最后一个数据被第一个读出来）。

可以参照下图去理解

2.栈的模拟实现

其实栈是一个比较简单且容易实现的数据结构，我们主要需要实现的功能有：

1.pop 返回并弹出栈顶元素

2.peek 返回栈顶元素

3.push 向栈顶插入一个元素

4. empty 判断栈是否为空

5.size 获取栈的大小

下面我们直接看到代码 

push：

public void push(int val){if(isFull()){//如果栈已满则扩容this.elem=Arrays.copyOf(this.elem,2*this.elem.length);}this.elem[this.usedSize++]=val;//uswdSize代表当前栈大小，下标从0开始//++代表插入元素后栈顶指针向后位移1位}

 pop：

public int pop(){if(isEmpty()){throw new RuntimeException("当前栈为空");//栈为空则抛出异常}int ret=this.elem[usedSize-1];this.usedSize--;//栈顶指针前移，代表该元素被弹出return ret;}

peek:

public int peek(){if(isEmpty()) {throw new RuntimeException("栈为空！");}return this.elem[this.usedSize-1];}

剩余完整代码我将上传至gitee供大家参考：Stack: 模拟实现栈

3.栈的基本用法

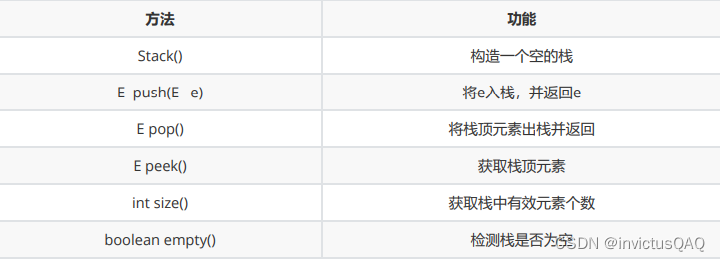
这里只是给大家简单介绍一下栈的常用方法，具体栈的使用我们会结合oj题目进行讲解

 4.部分栈有关oj解析

1.力扣

首先我们看到一道非常经典的逆波兰表达式求值，他的本质就是利用栈来模拟实现。

那么什么是逆波兰表达式呢？其实题目已经有了解释：

 可以看到题目已经明示我们要用栈，我们直接按照题意模拟即可。

 同时题目保证了表达式一定有效，我们可以省略处理算数异常的步骤。

思路：

对输入数据进行遍历，遇到数字则入栈，遇到运算符则取出栈顶的两个数字进行计算（注意先取出的元素位于操作符右侧），然后将结果压入栈中。由分析可知我们需要创建两个栈，一个用于存储运算符，另一个用于存储数字。

AC代码：

class Solution {public int evalRPN(String[] tokens) {Stack<Integer> stk=new Stack<>();for(int i = 0;i < tokens.length;i++){String x = tokens[i];if(!isOperations(x)) {stk.push(Integer.parseInt(x));}else{int num2=stk.pop();int num1=stk.pop();switch(x){case "+":stk.push(num1+num2);break;case "-":stk.push(num1-num2);break;case "*":stk.push(num1*num2);break;case "/":stk.push(num1/num2);break;}}}return stk.pop();}private boolean isOperations(String s) {//判断是否为操作符if(s.equals("+") || s.equals("-") || s.equals("*") || s.equals("/")) {return true;}return false;}}

 2.力扣

有效的括号这题同样是作为我们入门栈的一道非常经典的题目，题意很简单就是让我们判断输入的括号表达式是否为有效的。

 有一点我们需要注意到的是，左右括号必须以正确的顺序闭合

比如   ）（   和   (   [   )   ]   这两种都是不合法的

思路： 

1.遇到左括号时直接入栈，因为他需要与之后进来的右括号进行匹配

2.遇到右括号时与栈顶括号匹配，不符合则直接返回false，因为题目要求匹配顺序正确

3.在右括号匹配时注意判断栈是否为空，空则直接返回false

4.遍历完括号字符串后判断栈是否为空，为空说明匹配完成返回true，否则未能匹配完全返回false

AC代码

class Solution {public boolean isValid(String s) {Stack<Character> stack=new Stack<>();for(int i=0;i<s.length();i++){char ch=s.charAt(i);if(ch == '(' || ch == '[' || ch == '{') {//如果是左括号，就入栈stack.push(ch);}else{if(stack.empty()){return false;}else{char c=stack.peek();if(c == '(' && ch == ')' || c == '[' && ch == ']' || c == '{' && ch == '}' ){stack.pop();}else{return false;}}}}if(!stack.empty()) return false;else return true;}
}